FFT là viết tắt của Fast Fourier transform là một thuật toán tính nhanh của phép phân tích Fourier. Mình không giỏi lắm về cái này đâu, dưới đây là một số kiến thức mình tự cóp nhặt và tham khảo được từ nhiều nơi, nay chia sẻ lại cho các bạn theo hiểu biết của mình nên chắc chắn có nhiều sai sót mong được góp ý để hoàn thiện hơn
Mạch nháy theo nhạc là gì ?
Đơn giản là mạch có khối led nhấp nháy lên xuống hoặc các hiệu ứng biến tấu theo điệu nhạc. Chúng ta có 2 cách cơ bản để tạo ra hiệu ứng nháy theo nhạc là:
- Nháy theo điện áp ( VU master), mạch này chỉ đơn giản là đọc điện áp đầu vào, nếu lớn thì cho hiệu ứng mạnh còn nhỏ thì hiệu ứng yếu. Đây là mạch nháy rất đơn giản và có 1 số ic chuyên dụng như AN6884
- Nháy theo phổ tần số, chúng ta phân tích phổ của âm thanh rồi đưa ra các hiệu ứng nháy tương ứng (Spectrum analyzer)
Sóng âm
1 dao động âm thuần túy có thể biểu diễn dưới dạng hình SIN
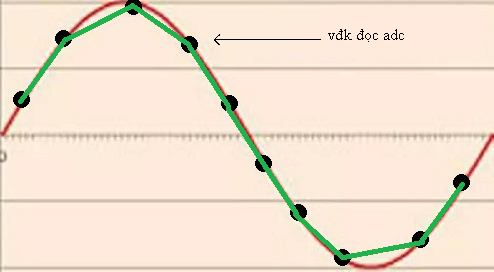
Khi micro nhận được dao động âm này, nó chuyển thành điện áp dao động theo hình SIN, bộ vi điều khiển đọc ADC để lưu lại điện áp tại thời điểm đó, nhưng vi điều khiển không thể đọc 1 cách liên tục được mà phải cách nhau 1 khoảng, khoảng thời gian này chính là thời gian giữa 2 lần lấy mẫu
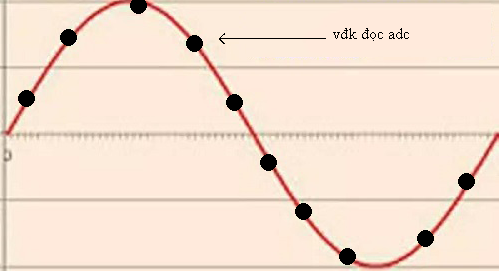
Và đối với vi điều khiển thì sóng hình SIN đó sẽ trông như đường màu xanh

Thời gian chúng ta lấy mẫu càng nhanh thì được càng nhiều điểm (mẫu) và đường màu xanh càng mềm mại hơn và càng gần giống với hình SIN hơn.
Như vậy, chúng ta có 2 khái niệm:
- Thời gian lấy mẫu ( hay chu kì lấy mẫu)
- Tần số lấy mẫu ( tức nghịch đảo của thời gian lấy mẫu)
Âm thanh trong không khí
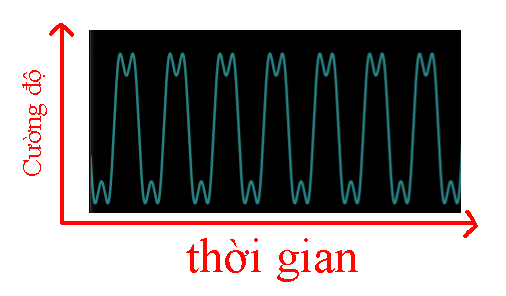
Âm thanh thông thường là hỗn hợp của hàng tá các dao động như trên. Ví dụ 1 âm thanh là hỗn hợp của sóng âm có tần số 10hz và 30hz – có cường độ (hoặc biên độ) = 1/3 sẽ có dạng như sau:
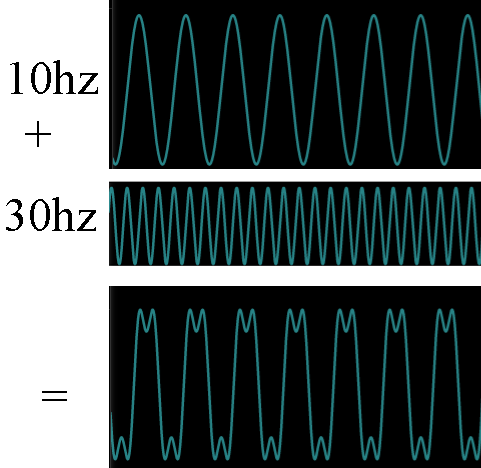
Đồ thị chúng ta có được là đồ thị kết hợp của sóng âm 10hz + 30hz ( có cường độ = 1/3) và được biểu diễn theo hệ tọa độ cường độ – thời gian
Phép biến đổi Fourier
Chúng ta có thể dùng Biến đổi Fourier để biến đổi trục thời gian của đồ thị sang trục tần số
Nói 1 cách đơn giản, đồ thị trên sau khi biến đổi sẽ trở thành như này:
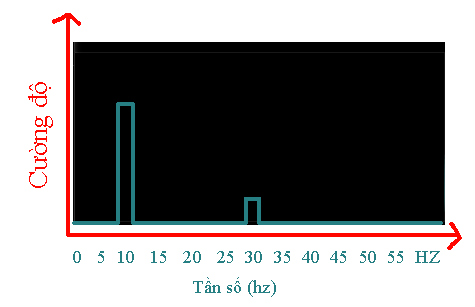
Sóng 10hz có cường độ gấp 3 lần sóng 30hz nên đương nhiên cột sóng của 10hz cao gấp 3 lần cột sóng 30hz. Các tần số khác không xuất hiện nên có cường độ bằng 0
Tóm lại: Khi chúng ta lấy mẫu ADC của âm thanh theo 1 chu kì / tần số nhất định, ta có được 1 đồ thị sóng âm ở dạng nguyên bản ( cường độ – thời gian), khi đưa đồ thị này vào hàm biển đổi fourier ta được đồ thị ( cường độ – tần số)
Cách tính fourier
Toán học Fourier có 3 dạng dạng biến đổi cơ bản
- Biến đổi Fourier liên tục
- Chuỗi Fourier
- Biến đổi Fourier rời rạc (DFT)
Chúng ta sẽ sử dụng dạng biến đổi Fourier rời rạc (DFT) để tính fourier
Phép biến đổi DFT
Độ phức tạp trong tính toán
Độ phức tạp ở đây ý là số lượng phép tính cần được tính để biến đổi DFT, điều này còn liên quan tới số lượng “mẫu” bạn mang đi thực hiện biến đổi. Số lượng mẫu đem đi biến đổi tạo ra các đặc điểm sau:
- Càng nhiều mẫu thì càng phức tạp (tính càng lâu), cụ thể với N mẫu (điểm) đòi hỏi N2 phép tính
- Càng nhiều mẫu thì việc phân tích càng chính xác
Hãy xem xét cụ thể yêu cầu bài toán của bạn để quyết định xem bao nhiêu mẫu mang đi tính là hợp lí. Ví dụ, bạn cần phân tích phổ của 1 bài hát. Bộ phân tích phải phân tích được các tần số từ 0 đến 15Khz, sai số cho phép là 200hz.
Giả sử, bạn cho bộ điều khiển lấy mẫu với tần số 20Khz và bạn phân tích với 64 mẫu, sai số của phép phân tích sẽ là: 20Khz / 64 = 312,5hz. Sai số quá lớn, vậy phải tăng số mẫu lên 128 thì sai số sẽ còn 20Khz/128=156,25 hz => đạt yêu cầu !
Nhưng cũng với 64 mẫu, bạn giảm tần số lấy mẫu xuống còn 10Khz, sai số là 10Khz/64 = 156,25 => đạt yêu cầu. Tuy nhiên, bạn không thể lấy mẫu ở 10Khz được, vì với tần số lấy mẫu 10Khz thì không thể phân tích được trong dải từ 0->15Khz như đề bài yêu cầu
P/s: Cách mình dùng từ sai số có thể không chính xác, các bạn đã biết chút về FFT có thể hiểu nó như số bước
Cách tính DFT
(từ chỗ này thím nào ngày xưa lười học toán đọc không hiểu thì về hỏi cô giáo ấy đừng hỏi mình nha :v)
Với tín hiệu đầu vào là 1 mảng N số thực ( chạy từ 0 đến n), biển đổi DFT đưa ra 1 mảng N số phức ( chạy từ 0 đến k )
Tại điểm đầu vào n, ta có giá trị đưa vào là x(n) và giá trị đưa ra là số phức X(k)

Với:

Suy ra:
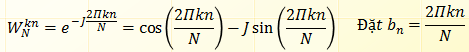
( P/s: Sử dụng công thức Euler để loại bỏ cơ số e)
Ta được
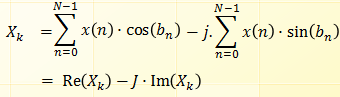
Viết X(k) dưới dạng tọa độ cực, ta được biên độ(cường độ) A(k) bằng cách lấy module số phức và pha bằng cách lấy argument của số phức X(k)
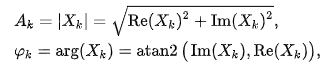
Bơ phệch, vậy là với N mẫu mang vào phân tích, chúng ta đã lấy được N cường độ
Ví dụ
Phân tích 1 tín hiệu sin có biên độ là 1, dao động với tần số 1hz. Dải phân tích là 0hz -> 7hz. Tần số lấy mẫu là 8hz, sai số 1hz => số mẫu mang đi phân tích sẽ là: 8/1 = 8 mẫu
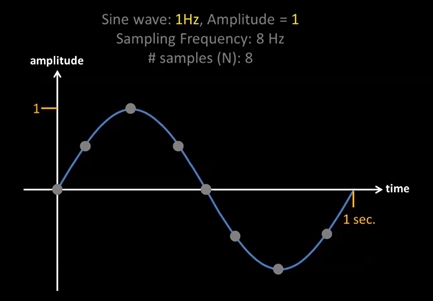
Biên độ đo được tại 8 điểm
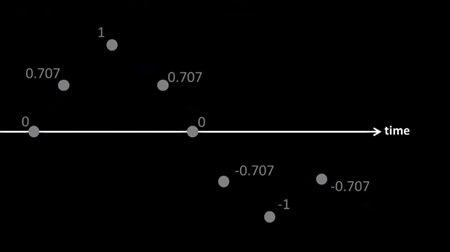
Dùng công thức
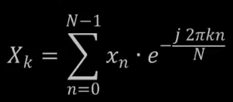
để tính DFT cho 8 điểm này
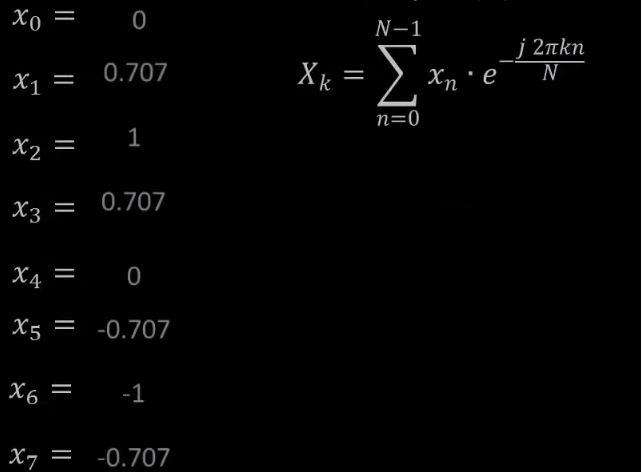
Kết quả tính DFT của 8 điểm
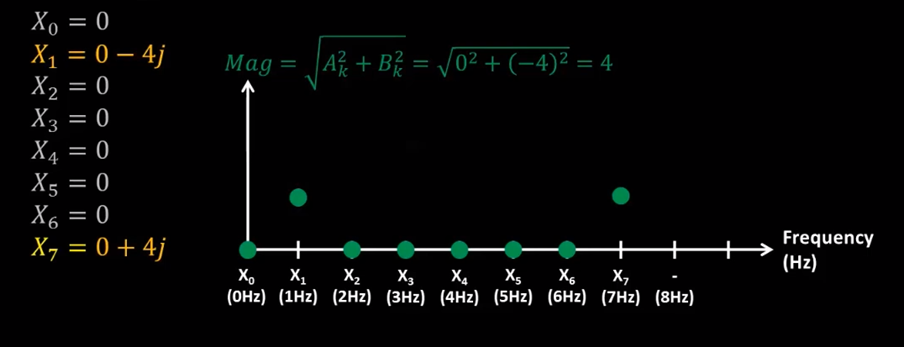
Từ miền tần số này ta có thể biết được tín hiệu ban đầu là cộng hợp của 2 sóng sin biên độ 4/8 và 4/8 tại tần số 1Hz và 7Hz, độ lệch pha -π/2 và π/2
Thuật toán FFT
Như đã nói ở trên đầu bài, đây là 1 phương pháp hiệu quả để giảm số lượng phép tính của DFT từ N2 phép tính xuống N log N phép tính
Phương pháp radix-2
Là 1 trong những phương pháp của giải thuật FFT với số điểm mang vào tính phải tuân theo quy luật N = 2 mũ s (với s là số nguyên dương)
Đại khái số điểm phải là 2 4 8 16 32 64 128 256 512 1024 2048 …
Biến đổi công thức DFT ta sẽ có:
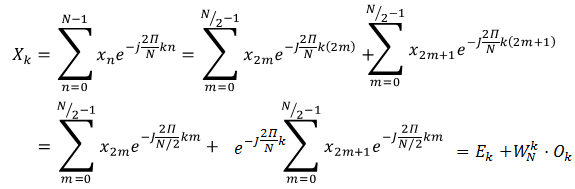
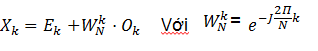
Biến đổi với k = k +N/2 thu được:
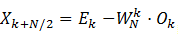
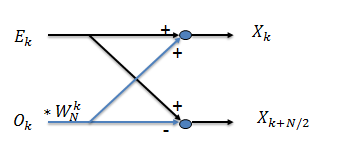
Ta được:
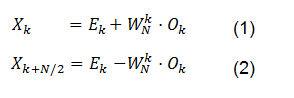

Sơ đồ biểu diễn cho 2 phương trình trên ( biểu đồ cánh bướm)
Ví dụ
Tính FFT cho 8 điểm, sử dụng biểu đồ cánh bướm như sau:
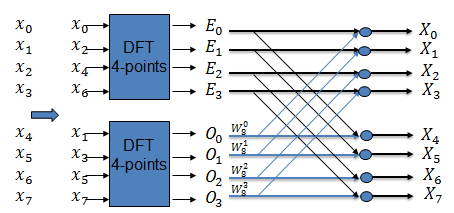
Cứ tiếp tục chia đôi phần chẵn và phần lẻ cho đến khi chỉ cần tính DFT của 2 điểm
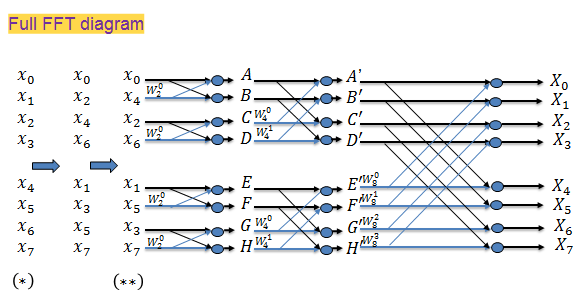
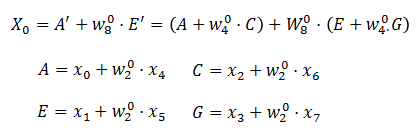
Nghịch đảo
Từ chuỗi (*) sang chuỗi (**) phải được nghịch đảo trọng số của bit. Ví dụ 1 số nhị phân có giá trị 0110.1011 sẽ được nghịch đảo thành 1101.0110 ( abcdefgh -> hgfedcba)
Tính đối xứng
Dữ liệu đầu ra được tính từ giá trị thứ 1 ( giá trị thứ 0 bỏ), dữ liệu đầu ra bị đối xứng qua tần số giới hạn = tần số lấy mẫu / 2
Tức là bạn lấy mẫu ở tần số 20Khz thì dải đo được chỉ giới hạn từ 0->10Khz thôi. Nói cách khác để đo được dải từ 0 -> 15Khz cần phải lấy mẫu ít nhất 30Khz
Lập trình tính FFT
Nếu đã hiểu cách tính FFT thì các bạn tự viết được chương trình thôi. Còn nếu bạn nào chưa hiểu thì cứ lấy code của mình mà xài, tính toán cũng khá ok, khá nhanh, bạn nào có chương trình hay hơn thì share mẹ đê giấu giấu cái con c*c : v !
Dưới đây là giải thuật tính FFT cơ bản cho 128 điểm được viết trên ngôn ngữ C. Các bạn có thể chạy nó trên các phần mềm như Cfree, DEV-C, Code-block …
FFT được tính trên tập số phức nên cần có 1 mảng lưu phần ảo và và phần thực. Các phép tính bên dưới chỉ đơn giản là công trừ nhân chia số phức cơ bản. Trong quá trình tính, bắt buộc phải sử dụng sin, cos, nhưng mà cho vi điều khiển tính sin cos thì có mà đái ra máu nên mình tính sẵn trên máy tính rồi cho vào bảng tra.
Ngoài ra FFT cũng phải làm việc với kiểu dữ liệu float rất nhiều, vi điều khiển tính float cũng muốn khóc, mà float ở đây thì toàn là các số từ -1 đến 1 thôi nên minh nhân tất cả các kiểu float với 100 (bao gồm cả bảng tra) để chuyển hết về dạng số nguyên. Lát tính xong chỉ việc chia lại cho 100
Lập trình cho vi điều khiển thì cứ phương châm này mà chơi: No sin cos, no float
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 |
#include <stdio.h> #include <math.h> #define N 128 #define PI 3.1415926535897 #define log2N 7 int RE[N]= { 786, 816, 837, 849, 850, 838, 814, 780, 744, 700, 653, 601, 550, 501, 484, 451, 426, 409, 398, 394, 396, 404, 415, 431, 451, 477, 479, 512, 550, 593, 641, 687, 730, 772, 806, 832, 851, 852, 847, 830, 803, 764, 482, 470, 439, 420, 403, 395, 394, 397, 405, 418, 436, 458, 483, 486, 520, 561, 607, 651, 698, 742, 778, 811, 830, 846, 848, 836, 814, 782, 744, 701, 653, 603, 552, 503, 486, 453, 427, 409, 399, 394, 395, 401, 414, 429, 448, 472, 473, 506, 544, 586, 633, 678, 722, 763, 798, 825, 842, 849, 843, 826, 798, 762, 722, 676, 627, 576, 526, 480, 468, 437, 416, 404, 396, 394, 398, 407, 420, 438, 461, 488, 492, 527, 567, 612, 658, 706, }; int IM[N]; // bang tra cuu Sin(a) cho FFT 128 diem const signed char Sin_table[511] = { 0, // Temp_N = 2 0,-100, // Temp_N = 4 0,-71,-100,-71, // Temp_N = 8 0,-38,-71,-92,-100,-92,-71,-38, // Temp_N = 16 0,-20,-38,-56,-71,-83,-92,-98,-100,-98,-92,-83,-71,-56,-38,-20, // Temp_N = 32 0,-10,-20,-29,-38,-47,-56,-63,-71,-77,-83,-88,-92,-96,-98,-100,-100,-100,-98,-96,-92,-88,-83,-77,-71,-63,-56,-47,-38,-29,-20,-10, // Temp_N = 64 0,-5,-10,-15,-20,-24,-29,-34,-38,-43,-47,-51,-56,-60,-63,-67,-71,-74,-77,-80,-83,-86,-88,-90,-92,-94,-96,-97,-98,-99,-100,-100,-100,-100,-100,-99,-98,-97,-96,-94,-92,-90,-88,-86,-83,-80,-77,-74,-71,-67,-63,-60,-56,-51,-47,-43,-38,-34,-29,-24,-20,-15,-10,-5, // Temp_N = 128 }; // bang tra cuu Cos(a) cho FFT 128 diem const signed char Cos_table[511] = { 100, // Temp_N = 2 100,0, // Temp_N = 4 100,71,0,-71, // Temp_N = 8 100,92,71,38,0,-38,-71,-92, // Temp_N = 16 100,98,92,83,71,56,38,20,0,-20,-38,-56,-71,-83,-92,-98, // Temp_N = 32 100,100,98,96,92,88,83,77,71,63,56,47,38,29,20,10,0,-10,-20,-29,-38,-47,-56,-63,-71,-77,-83,-88,-92,-96,-98,-100, // Temp_N = 64 100,100,100,99,98,97,96,94,92,90,88,86,83,80,77,74,71,67,63,60,56,51,47,43,38,34,29,24,20,15,10,5,0,-5,-10,-15,-20,-24,-29,-34,-38,-43,-47,-51,-56,-60,-63,-67,-71,-74,-77,-80,-83,-86,-88,-90,-92,-94,-96,-97,-98,-99,-100,-100, // Temp_N = 128 }; //Nghich dao cho FFF 128 diem void nghich_dao() // du lieu adc doc duoc can phai dua qua ham nay de xu li (goi ham nay 1 lan duy nhat truoc khi tinh FFT) { unsigned int i; i=RE[ 1]; RE[ 1]=RE[ 64]; RE[ 64]=i; i=RE[ 2]; RE[ 2]=RE[ 32]; RE[ 32]=i; i=RE[ 3]; RE[ 3]=RE[ 96]; RE[ 96]=i; i=RE[ 4]; RE[ 4]=RE[ 16]; RE[ 16]=i; i=RE[ 5]; RE[ 5]=RE[ 80]; RE[ 80]=i; i=RE[ 6]; RE[ 6]=RE[ 48]; RE[ 48]=i; i=RE[ 7]; RE[ 7]=RE[112]; RE[112]=i; i=RE[ 9]; RE[ 9]=RE[ 72]; RE[ 72]=i; i=RE[ 10]; RE[ 10]=RE[ 40]; RE[ 40]=i; i=RE[ 11]; RE[ 11]=RE[104]; RE[104]=i; i=RE[ 12]; RE[ 12]=RE[ 24]; RE[ 24]=i; i=RE[ 13]; RE[ 13]=RE[ 88]; RE[ 88]=i; i=RE[ 14]; RE[ 14]=RE[ 56]; RE[ 56]=i; i=RE[ 15]; RE[ 15]=RE[120]; RE[120]=i; i=RE[ 17]; RE[ 17]=RE[ 68]; RE[ 68]=i; i=RE[ 18]; RE[ 18]=RE[ 36]; RE[ 36]=i; i=RE[ 19]; RE[ 19]=RE[100]; RE[100]=i; i=RE[ 21]; RE[ 21]=RE[ 84]; RE[ 84]=i; i=RE[ 22]; RE[ 22]=RE[ 52]; RE[ 52]=i; i=RE[ 23]; RE[ 23]=RE[116]; RE[116]=i; i=RE[ 25]; RE[ 25]=RE[ 76]; RE[ 76]=i; i=RE[ 26]; RE[ 26]=RE[ 44]; RE[ 44]=i; i=RE[ 27]; RE[ 27]=RE[108]; RE[108]=i; i=RE[ 29]; RE[ 29]=RE[ 92]; RE[ 92]=i; i=RE[ 30]; RE[ 30]=RE[ 60]; RE[ 60]=i; i=RE[ 31]; RE[ 31]=RE[124]; RE[124]=i; i=RE[ 33]; RE[ 33]=RE[ 66]; RE[ 66]=i; i=RE[ 35]; RE[ 35]=RE[ 98]; RE[ 98]=i; i=RE[ 37]; RE[ 37]=RE[ 82]; RE[ 82]=i; i=RE[ 38]; RE[ 38]=RE[ 50]; RE[ 50]=i; i=RE[ 39]; RE[ 39]=RE[114]; RE[114]=i; i=RE[ 41]; RE[ 41]=RE[ 74]; RE[ 74]=i; i=RE[ 43]; RE[ 43]=RE[106]; RE[106]=i; i=RE[ 45]; RE[ 45]=RE[ 90]; RE[ 90]=i; i=RE[ 46]; RE[ 46]=RE[ 58]; RE[ 58]=i; i=RE[ 47]; RE[ 47]=RE[122]; RE[122]=i; i=RE[ 49]; RE[ 49]=RE[ 70]; RE[ 70]=i; i=RE[ 51]; RE[ 51]=RE[102]; RE[102]=i; i=RE[ 53]; RE[ 53]=RE[ 86]; RE[ 86]=i; i=RE[ 55]; RE[ 55]=RE[118]; RE[118]=i; i=RE[ 57]; RE[ 57]=RE[ 78]; RE[ 78]=i; i=RE[ 59]; RE[ 59]=RE[110]; RE[110]=i; i=RE[ 61]; RE[ 61]=RE[ 94]; RE[ 94]=i; i=RE[ 63]; RE[ 63]=RE[126]; RE[126]=i; i=RE[ 67]; RE[ 67]=RE[ 97]; RE[ 97]=i; i=RE[ 69]; RE[ 69]=RE[ 81]; RE[ 81]=i; i=RE[ 71]; RE[ 71]=RE[113]; RE[113]=i; i=RE[ 75]; RE[ 75]=RE[105]; RE[105]=i; i=RE[ 77]; RE[ 77]=RE[ 89]; RE[ 89]=i; i=RE[ 79]; RE[ 79]=RE[121]; RE[121]=i; i=RE[ 83]; RE[ 83]=RE[101]; RE[101]=i; i=RE[ 87]; RE[ 87]=RE[117]; RE[117]=i; i=RE[ 91]; RE[ 91]=RE[109]; RE[109]=i; i=RE[ 95]; RE[ 95]=RE[125]; RE[125]=i; i=RE[103]; RE[103]=RE[115]; RE[115]=i; i=RE[111]; RE[111]=RE[123]; RE[123]=i; } void FFT() //ham tinh FFT { int thuc_W, ao_W ; int temp_N=2,index=1,dem=0; int thuc_Ek,ao_Ek,KQ_thuc,KQ_ao; for(int buoc=0;buoc<log2N;buoc++) { for(int k=0;k<index;k++) { thuc_W = Cos_table[dem]; ao_W = Sin_table[dem]; for(int i=k;i<N;i+=temp_N) { thuc_Ek = RE[i]; ao_Ek = IM[i]; KQ_thuc = (thuc_W * RE[i+index] - ao_W * IM[i+index])/100; KQ_ao = (thuc_W * IM[i+index] + RE[i+index] * ao_W)/100; RE[i] = thuc_Ek + KQ_thuc; RE[i+index] = thuc_Ek - KQ_thuc; IM[i] = ao_Ek + KQ_ao; IM[i+index] = ao_Ek - KQ_ao; } dem++; } index <<=1; temp_N <<=1; } } int main() { nghich_dao(); FFT(); printf("Ket qua tinh toan FFT:\n"); for(int x = 0; x < N; x++) printf("%i + %ii\n,", RE[x],IM[x]); printf("\n"); int y_y=0; for (int i=1;i<128;i++) { RE[y_y] = sqrt(RE[i] * RE[i] + IM[i] * IM[i]); // tinh Ak y_y++; printf("%i",RE[y_y]); } return 0; } |
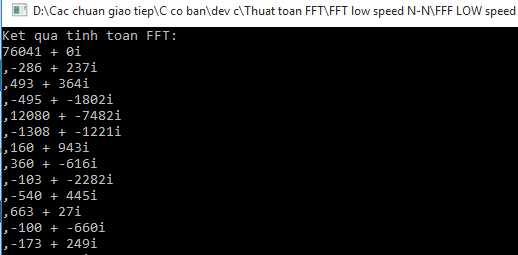
Hàm nghịch đảo bit có thể viết ngắn gọn lại bằng vòng lặp, trông code sẽ gọn hơn, nhưng làm như mình thì tốc độ chạy của chip sẽ nhanh hơn nhiều là dùng vòng lặp đó !
1 số công cụ tiện ích, Chia sẽ cho các bạn 1 số tool hay để sinh mã code nhanh gọn lẹ, bao gồm tool để tạo bảng tra sin cos, tool để sinh code cho hàm nghịch đảo
Các bạn tải 3 tool tiện tích tại đây
Cách sử dụng: Mởi tool lên và điền vào log2N của số điểm mà bạn muốn mang đi tính FFT, ví dụ bạn tính FFT 128 điểm thì log2N = 7, điền 7 vô và gõ enter và nó sẽ sinh code cho bạn
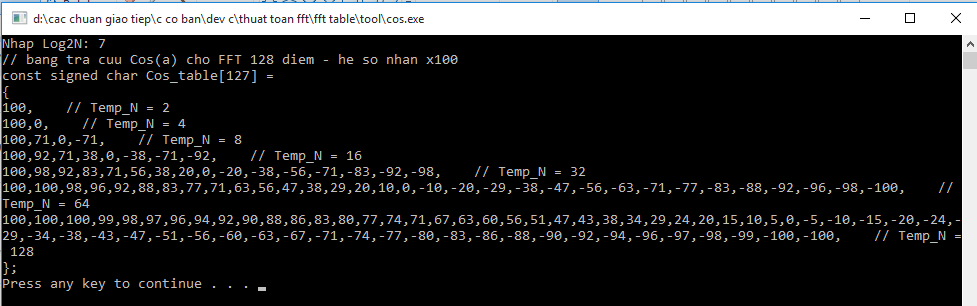
Còn đây là mã nguồn của mấy cái tool đó được viết bằng DEV C++, tải tại đây
Demo chương trình nháy theo nhạc – Audio Spectrum analyzer với ma trận led P5 full color và chip stm32f103c8t6
Nếu lấy tín hiệu từ cổng line thì chỉ cần qua con tụ lọc 4.7uf rồi vào đọc ADC luôn, còn qua mic thì các bạn làm tạm 1 mạch khuyếch đại xài OPAM như sau:
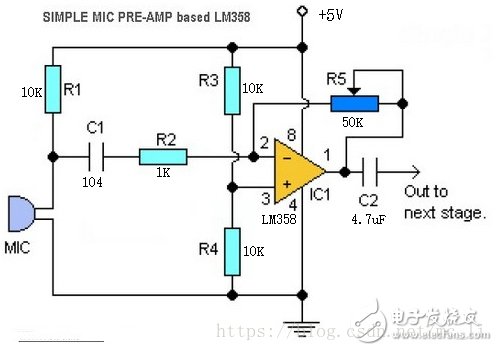
Còn đây là project tạm bợ của mình, tính FFT 512 điểm rồi xuất ra led luôn chứ chưa qua lọc,cắt phổ hay thêm hiệu ứng gì hết …
Tải Code mẫu tại đây
Chào bạn, bài viết của bạn rất có tính xây dựng và chia sẻ. Tuy nhiên có vài điểm mình thấy bạn nói không đúng, mình xin được góp ý như sau để bạn có thể cải thiện và chia sẽ với mọi người tốt hơn.
1. 1 sóng âm thuần túy có dạng hình SIN
-> Sóng âm không có dạng hình sin. Có thể dùng FT để biến đổi sóng âm thành tổng các sóng sin, nhưng đó chỉ là với tín hiệu tuần hoàn. Với tín hiệu không tuần hoàn, ta chỉ coi như nó tuần hoàn trên một khoảng nhỏ để biến đổi. Nhưng tóm lại sóng âm không phải cái nào cũng có dạng hình sin (phần lớn). Giả sử tiếng rơi của cây bút xuống bàn, âm thanh đó không tuần hoàn, và không có dạng sin.
1. Âm thanh thông thường là hỗn hợp của hàng tá các sóng hình sin như trên.
-> Như câu 1 đã giải thích ở trên. Tiếng cây bút rơi xuống bàn không phải là hỗn hợp của các sóng sin. Trong xử lý tín hiệu âm thanh, người ta chỉ lấy một đoạn nhỏ (20 – 50 ms) và coi như nó tuần hoàn để phân tích.
2. Biến đổi Fourier có tác dụng biến đổi trục thời gian của đồ thị sang trục tần số
-> Biến đổi Fourier có tác dụng phân tích tín hiện thành thành phần tần số của nó, nó không hề biến thời gian thành tần số mà là tín hiệu thành tần số.
3. Như đã nói ở trên, bộ vi điều khiển của chúng ta chỉ có thể đọc các tín hiệu ADC 1 cách rời rạc theo 1 khoảng thời gian lấy mẫu nhất định. Do vậy chúng ta sẽ sử dụng dạng biến đổi Fourier rời rạc (DFT) để tính fourier
-> tín hiệu vào rời rạc sẽ có phân tích DTFT tức là discrete time fourier transform, tức là FT cho tín hiệu rời rạc. DFT là sự lấy mẫu trên miền tần số của DTFT.
Mình chắc là bạn không nắm chắc về các khái niệm này của xử lý tín hiệu số
4. Sai số lấy mẫu?
-> mình chắc chắn bạn không biết đến khái niệm về cửa sổ (window function), độ rộng cửa sổ, hay zero padding. Sai số (độ phân giải) của tần số phụ thuộc số điểm tính FFT. Dù chỉ tính trên cửa sổ gồm 64 mẫu, nhưng thêm vào đằng sau 64 số 0 nữa thì vẫn có thể có được sai số nhỏ như đang tính với cửa sổ 128 mẫu. độ rộng của cửa sổ thì tùy thuộc vào chu kỳ của thành phần tần số muốn lấy.
Mình rất hoan nghênh tinh thần chia sẽ của bạn. Tuy nhiên nếu chưa nắm rõ bạn có thể chỉ chia sẽ code, cái này chỉ cần nhìn công thức là làm được. Giải thích quá nhiều nhưng không chính xác dẫn đến sự sai lệch trong tìm hiểu của người đọc.
Regards
Cảm ơn bác đã góp ý ! Đây không phải lĩnh vực chuyên sâu của mình nên chắc chắn có nhiều sai sót, kiến thức của mình cũng là cóp nhặt chứ không phải học hành bài bản, sau khi đọc các chia sẻ của bác thì hầu hết những thứ bác nói mình đều đã tìm hiểu. Tuy nhiên mục đích của bài viết “Thuật toán FFT cho mạch nháy theo nhạc” không phải là nghiên cứu sâu về FFT hay biến đổi Fourier mà là giải thích 1 cách cơ bản dễ hiểu nhất cho người không được học cao cũng hiểu. Các chia sẻ của mình có thể không hoàn toàn chính xác với các định nghĩa hàn lâm nhưng là cách đơn giản nhất để hiểu cơ bản cách hoạt động và đó là mục đích của mình khi viết bài này !
Bài viết còn có một số từ khiếm nhã. Thực ra bạn hiểu chưa kĩ về xử lý tín hiệu, chỗ “Độ phức tạp trong tính toán” ở ví dụ bạn cần tìm hiểu về định lý lấy mẫu. Đâm ra code của bạn bị lủng củng khi bạn giấu tool, thiếu sự mạch lạc khi code thuật toán nói chung và thuật toán xử lý số tín hiệu nói riêng. Các bạn có thể dùng code trên nếu muốn làm cho vui chứ không khuyến khích dùng để nghiên cứu.
bạn ơi, sau khi b tính FFT 512 điểm, làm sao b biểu diễn ra led được vậy, mình thấy dàn led của chỉ có khoảng 50 đến 60 cột thôi
bạn cứ lấy 1:(uint8_t)(512/60):512 là được thôi